Variable aléatoire et Loi de Probabilité
Voir aussi : Lois continues - Schéma et loi de Bernoulli - Loi uniforme - Loi exponentielle - Loi Binomiale
Définition 1
Une expérience aléatoire est une expérience
dont on ne peut prédire le résultat.
Définition 2
Une expérience aléatoire dont les résultats possibles sont des nombres réels est appelée variable aléatoire.
Définition 3
Soit X une variable aléatoire.
La fonction qui à toute valeur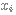 
prise par la variable aléatoire lui associe la probabilité 
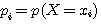est appelée loi de probabilité.
Remarque
En général, la loi de probabilité d'une variable aléatoire prenant un nombre fini de valeurs est donnée sous forme d'un tableau :
|
Valeurs xi |
x1 |
x2 |
x3 |
...... |
xn |
|
p(X=ki) |
p1 |
p2 |
p3 |
...... |
pn |
Définition
L'espérance d'une variable aléatoire prenant un nombre fini de valeurs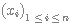 
pondérées par les probabilités 
est donnée par la formule 
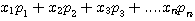
Variance d'une loi de probabilité prenant un nombre fini de valeurs
Définition
La variance d'une variable aléatoire prenant un nombre fini de valeurs est, avec les notations précédentes définie par 
où E est l'espérance de la variable aléatoire.